Calculation of Load Acting on a Shaft
The load from earth pressure and surcharge are computed in the frame "Load analysis". The stiffness of the shaft has a major influence on earth pressure. The rigid structure does not allow deformation, so the earth pressure is much higher than on the flexible shaft.
Three types of shafts can be modeled in the program:
- Flexible - spatial active pressure is considered (earth pressure, surface surcharge and local surcharge)
- Semirigid
- Rigid - spatial pressure at rest is considered (earth pressure, surface surcharge and local surcharge)
Ways of load determination
Load from earth pressure and surface surcharge acts as a uniform load on the entire diameter. This load causes structure stress only by normal force - bending moment on the shaft is theoretically equal to zero. For modeling of real behavior of the shaft, the program introduces the Reduction coefficient in compliance to the standards DIN V 4034-1 or СНиП II-94-80. The recommended value of a reduction coefficient is 25 %.
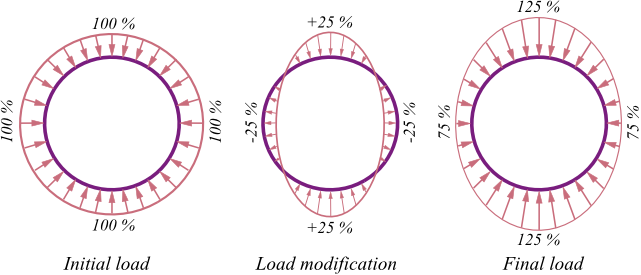 Modification of uniform load by reduction coefficient
Modification of uniform load by reduction coefficient
Load from a local surcharge is considered as shown in the next picture. This load is not modified by the reduction coefficient.
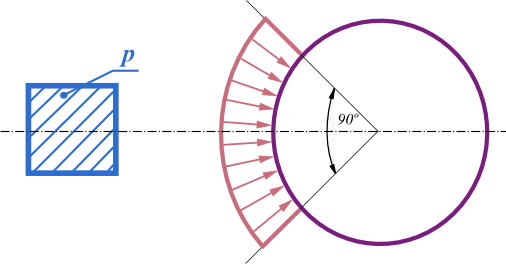 Load from a local surcharge
Load from a local surcharge
Recalculation of the load on walers
If the walers are input the program computes the load on each of them. The load depends on the axial distance between walers as shown in the picture.
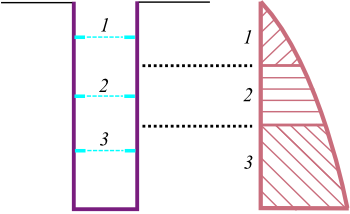 Calculation of load on the waler
Calculation of load on the waler
If no walers are input, the program computes load on unit depth (1 m, 1 ft).
If load is calculated, then program determines the distribution of internal forces on structure of the shaft.
Literature:
Berezantzev, V. G.: Earth pressure on the cylindrical retaining walls, Brussels conference on Earth pressure problems, 1958.
ČSN 73 0037: Zemní tlak na stavební konstrukce, 1990.
DIN 4085: Berechnung des Erddrucks, 1987.
Exner, K.: Hloubení jam, VŠB v Ostravě, 1986.
Cheng, Y. M.; Hu, Y. Y.: Active earth pressure on circular shaft lining obtained by simplified slip line solution with general tangential stress coefficient. Chinese Journal of Geotechnical Engineering, 27 (1), 110-115, 2005.
Link, H.; Lutgendorf, H.; Stoss, K.: Richtlinien zur Berechnung von Schachtauskleidungen in nicht standfestem Gebirge, 1976.
Sedláček, M.: Zatížení kruhových šachet prostorovým zemním tlakem. Příspěvek ke konferenci Zakládání staveb, 2014.
Snášelová, K.: Hloubení a vyztužování jam v extrémních podmínkách, ODIS VTEI pro uhelný průmysl, 1987.
Tobar, T.; Meguid, M.: Distribution of active earth pressure on vertical shafts, Geo Halifax, 2009.
Valencia, T. T.: An experimental study of the earth pressure distribution on cylindrical shafts, McGill University, Montreal, 2009.
Walz, B.; Pulsfort, M.: Raumliche Erddruck auf Schachtbauwerke in Abhangigkeit von der Wandverformung, Bergische Universitat Wuppertal, 1999.