Elastic-perfectly plastic models
The elastic-perfectly plastic material models assume that the yield surface remains constant during plastic flow.
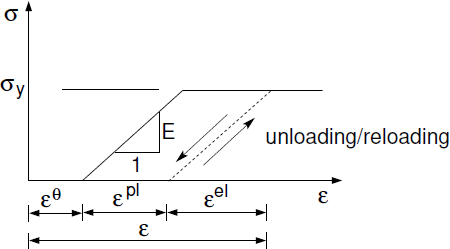
This is schematically illustrated in the stress-stress diagram, where σy represents the yield strength separating an elastic and plastic response. When arriving at the yield strength the stress at a given material point remains constant, i.e., σ = σy. On the other hand, elastic-plastic material models with hardening/softening allow for a gradual evolution of yield strength with the evolution of plastic strain.
Beyond the elastic limit the increment of overall strain Δε corresponds to the increment of plastic strain Δεpl. Unlike linear models the initial strain is a sum of the strain caused by a temperature change εθ = αΔθ, where α is the coefficient of thermal expansion, and plastic strain εpl, i.e., ε0 = εθ + εpl. The stress is calculated from the elastic part of the overall strain εel = ε - ε0, i.e., σ = Eεel. Determination of the plastic strain is driven by the selected type of the material model.
The class of elastic-perfectly plastic material models include the Drucker-Prager, Mohr-Coulomb, Hoek-Brown models.