Hoek-Brown
The Hoek-Brown material model is the most commonly used failure criterion to describe a nonlinear behavior of rock masses. Similarly to the Mohr-Coulomb material model, the Hoek-Brown model is formulated in terms of three failure functions with the projection into the deviatoric plane in the form of an irregular hexagon. However, unlike the Mohr-Coulomb model, the projection of the yield surface fHB into the meridian plane is described by a nonlinear function. It is obvious that similarly to the Mohr-Coulomb model the Hoek-Brown yield criterion is a function of the mean effective stress σmeff and the Lode angle θ.
 a) yield surface in principal stress space, b) projection into plane of maximum and minimum principal stress c) projection into deviatoric plane
a) yield surface in principal stress space, b) projection into plane of maximum and minimum principal stress c) projection into deviatoric plane
The Hoek-Brown model is purely empirical and its formulations grounds on the Geological strength index GSI (the value of GSI =100 corresponds to an intact rock and decreases to zero with worsening of the rock quality), the disturbance factor D (it takes into account prior underground activities including mining and excavation, the value of D=0 corresponds to an intact rock and the maximum degree of damage is represented by the value of D=1), the uniaxial compressive strength of an intact rock σci and parameter mi. The last two parameters are determined from the triaxial test. The physically acceptable maximum value of the prescribed tensile strength ![]() is given by
is given by
![]()
where the parameter s and the reduced Hoek-Brown constant mb are expressed in terms of parameters GSI and D as

Impact of individual parameters on the projection of the yield surface into the meridian plane is illustrated in the following figure.

The Hoek-Brown model requires introduction of the Modulus of elasticity of rock mass Erm, which takes into account the state of damage of the rock mass. It can be determined for example with the help of model parameters GSI, D and σci [2]
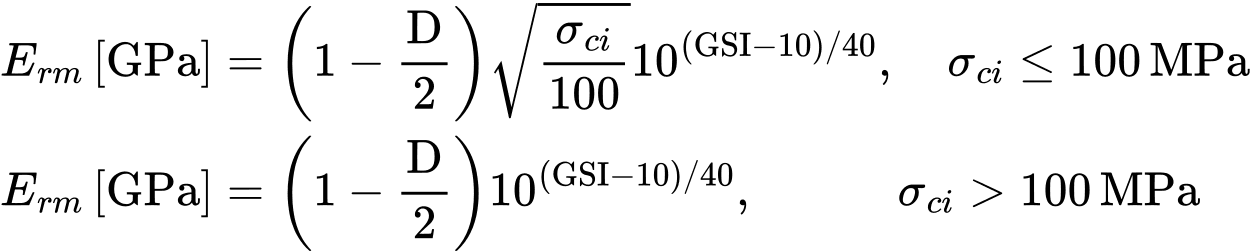
Further options are available in [3].
The model parameter a adjusting the power relation in the yield surface definition can also be determined using the geological strength index GSI as follows
![]()
The model parameters are presented in the following table.
Symbol | Units | Description | |
| [MPa] | Modulus of elasticity of rock mass | |
| [-] | Poisson's ratio | |
| [MPa] | Strength in uniaxial compression | |
| [-] | Hoek-Brown constant | |
GSI | [-] | Geological strength index | |
D | [-] | Disturbance factor | |
| [°] | Dilatancy angle (the initial value | |
| [kN/m3] | Bulk weight | |
| [-] | Reduced Hoek-Brown constant (specified or computed from GSI, D, | |
| [-] | Material constant ((specified or computed from z GSI, D) | |
| [kPa] | Maximum allowable tensile strength, | |
TsRF | [-] | Tensile strength reduction factor (0,1), if specified then | |
| [kPa] | Limiting value of confined pressure to model dilatancy | |
| [1/K] | Coefficient of thermal expansion (when considering temperature effects) |
The flow rule is similarly to the Drucker-Prager and Mohr-Coulomb models in general non-associated. Therefore, it allows for modeling dilatancy (evolution of positive volumetric plastic strains during plastic shearing) by introducing the dilatancy angle ψ. However, the dilation angle is not necessarily constant but may evolve as plotted in the following figure.
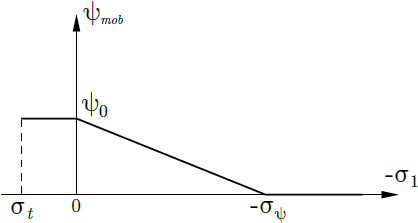
Implementation of the Hoek-Brown model automatically introduces the value of maximum tensile strength ![]() . This value can either be specified or computed based on the tensile strength reduction factor TsRF, recall the table of model parameters. Limiting the tensile strength is driven, similarly to the Mohr-Coulomb model, by the Rankin yield surface.
. This value can either be specified or computed based on the tensile strength reduction factor TsRF, recall the table of model parameters. Limiting the tensile strength is driven, similarly to the Mohr-Coulomb model, by the Rankin yield surface.
The Hoek-Brown model allows for performing the stability analysis. Both the standard slope stability analysis and stability analysis within a given construction stage can be carried out. However, unlike the Mohr-Coulomb model, the Hoek-Brown model introduces the parameter η reducing the uniaxial compressive strength σci. This parameter is expressed in terms of the reduction parameter ζ reducing in turn the shear strength parameters φ, c in models of the Mohr-Coulomb type. The Factor of safety FS is thus equal to ζ. Further details can be found in the theoretical manual.
Often posted analogy with the Mohr-Coulomb model is described in detail here. The response of Hoek-Brown model in comparison to the Mohr-Coulomb model is illustrated in the theoretical manual by simulating simple laboratory tests.
Implementation of the Hoek-Brown material model into the GEO5 FEM program is described in detail in the theoretical manual. Further information are available in the following literature.
Literature:
[1] E. Hoek and E.T. Brown, Practical estimates of rock mass strength, International Journal of Rock Mechanics and Mining Sciences, 34.8 (1997), 1165-1186
[2] E. Hoek, C. Carranza-Torres and B. Corkum, Hoek-Brown failure criterion - 2002 edition, Proceedings of the 5th North American symposium - NARMS-TAC (2002)
[3] E. Hoek, M.S Diederichs, Empirical estimation of rock mass modulus, International Journal of Rock Mechanics \& Mining Sciences, 43 (2006), 203-215