Passive Earth Pressure - The Rankine and Mazindrani Theory
Passive earth pressure follows from the following formula:
![]()
where: | σz | - | vertical geostatic stress |
Kp | - | coefficient of passive earth pressure due to Rankine | |
β | - | slope inclination | |
γ | - | weight of soil | |
z | - | assumed depth | |
| - | coefficient of passive earth pressure due to Mazindrani |
The coefficient of passive earth pressure Kp is given by:
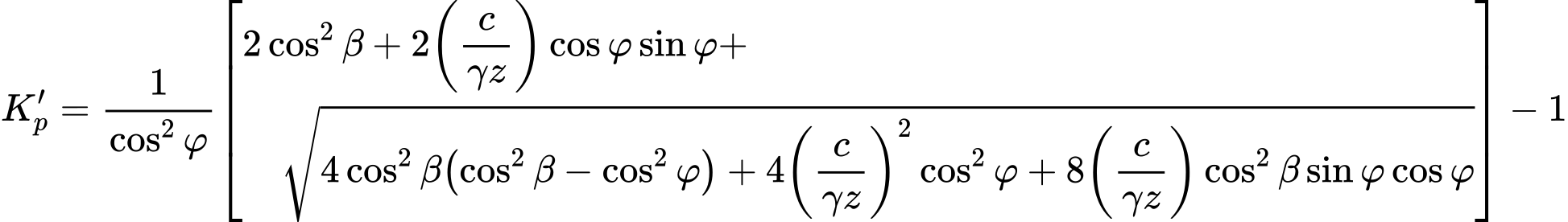
where: | β | - | slope inclination |
φ | - | angle of internal friction of soil | |
c | - | cohesion of soil |
If there is no friction (δ = 0) between the structure and cohesionless soils (c = 0), the ground surface is horizontal (β = 0) and the resulting slip surface is also plane with the slope:
![]()
The Mazindrani theory then reduces to the Rankine theory. The coefficient of passive earth pressure is then provided by:
![]()
where: | φ | - | angle of internal friction of soil |
Passive earth pressure σp by Rankine for cohesionless soils is given:
![]()
where: | γ | - | unit weight of soil |
z | - | assumed depth | |
Kp | - | coefficient of passive earth pressure due to Rankine |
Literature:
Mazindrani, Z.H., and Ganjali, M.H. 1997. Lateral earth pressure problem of cohesive backfill with inclined surface. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 123(2): 110-112.