Stress analysis options
The GEO5 FEM program performs the stress-strain analysis considering either drained or undrained conditons. The option of interest is selected when setting up a given material model. By default the application of drained conditions is expected. This option assumes a steady state of pore pressures (p = pss), i.e., the state at the end of consolidation at time ![]() . Suction is not taken into account. This means that above the ground water table the saturation degree S = 0, whereas below the ground water table we set S = 1. The analysis is carried out employing effective stresses together with effective shear strength parameters. The pore pressure enters the analysis as the prescribed loading. On the other hand, undrained conditions assume the analysis to be performed at the beginning of consolidation at time t = 0. As an example we may consider excavation in saturated soils with low permeability. The task generates excess pore pressures (p = pex). The GEO5 FEM program provides three options to adopt undrained conditions:
. Suction is not taken into account. This means that above the ground water table the saturation degree S = 0, whereas below the ground water table we set S = 1. The analysis is carried out employing effective stresses together with effective shear strength parameters. The pore pressure enters the analysis as the prescribed loading. On the other hand, undrained conditions assume the analysis to be performed at the beginning of consolidation at time t = 0. As an example we may consider excavation in saturated soils with low permeability. The task generates excess pore pressures (p = pex). The GEO5 FEM program provides three options to adopt undrained conditions:
Analysis in effective stresses (cef, φef)
This option (Type 1) is available to all material models. The analysis is carried in effective stresses while considering effective shear strength parameters. The basic material parameters describing the elastic behavior of the material, i.e., the modulus of elasticity and Poisson's ratio, correspond to the drained conditions. Grounding on the assumption of volumetric incompressibility the analysis introduces an effective stiffness matrix. Providing the solution considers introduction of ground water table or its change, the resulting value of pore pressure is a sum of steady state end excess pore pressure tlaku p = pss + pex. In material models, which address dilation with the help of dilatancy angle ψ (as well as the mobilized dilatancy angle ψm in Hardening soil model), the value of ψ is set to zero.
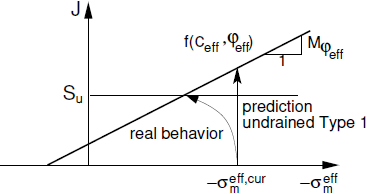
Unlike real behavior of soils this approach assumes that the effective stress does not change. This may predict a significantly overestimated value of the deviatoric stress at failure. The mobilized shear strength therefore exceeds the undrained shear strength of a given soil as evident from the figure below. The program allows visualization of numerically predicted undrained shear strength ![]() , where J is the equivalent deviatoric stress and θ is the Lode angle. This value should be maller than the real value of undrained shear strength
, where J is the equivalent deviatoric stress and θ is the Lode angle. This value should be maller than the real value of undrained shear strength ![]() . The user is advised to check this condition especially if adopting elastic-perfectly plastic material models.
. The user is advised to check this condition especially if adopting elastic-perfectly plastic material models.
Analysis in effective stresses (Su)
This option (Type 2) is available only to models of the Mohr-Coulomb type (Drucke-Prager, Mohr-Coulomb, Modified Mohr-Coulomb). The analysis is performed in analogy with the previous option including the formulation of effective stiffness matrix and determination of excess pore pressure. The resulting pore pressure is a sum of steady state and excess pore pressure p = pss + pex. The dilatancy angle ψ is again set to zero. The only difference, but rather essential, is the application of total shear strength parameters. The effective coefficient of cohesion c is replaced by the undrained shear strength Su(cu) and the angle of internal friction φ is assumed equal to zero (φu = 0).
From the computational point of view the Drucker-Prager yield function is replaced by the Mises yield function. Similarly, the Mohr-Coulomb yield function is replaced by the Tresca yield function. From the practical point of view, this option allows for taking into account the real value of Su as it is the input parameter. Nevertheless, the predicted pore pressures and thus also the effective stresses might not be entirely correct.
Analysis in total stresses (Su)
This option (Type 3) is available only to models of the Mohr-Coulomb type (Drucke-Prager, Mohr-Coulomb, Modified Mohr-Coulomb). The analysis is carried out in total stresses. Both the stiffness parameters (modulus of elasticity ![]() and Poisson's ratio
and Poisson's ratio ![]() and shear strength parameters
and shear strength parameters ![]() are assumed as total. If the K0 procedure is adopted it is expected that the generated stresses correspond to the total stresses.
are assumed as total. If the K0 procedure is adopted it is expected that the generated stresses correspond to the total stresses.
The potential change in steady state pore pressure ![]() in the soil found below the ground water table is not reflected in the analysis. The change in excess pore pressure
in the soil found below the ground water table is not reflected in the analysis. The change in excess pore pressure ![]() is also not generated and the current total pore pressure is set to zero, p = 0. The change in effective stresses thus corresponds to the change in total stresses. This is also reflected in graphical representation of these variables. The potential change in pore pressure thus cannot be visualized. The user should be aware of that.
is also not generated and the current total pore pressure is set to zero, p = 0. The change in effective stresses thus corresponds to the change in total stresses. This is also reflected in graphical representation of these variables. The potential change in pore pressure thus cannot be visualized. The user should be aware of that.