Podejście obliczeniowe według Masopusta
Krzywa obciążeniowa (obciążenie-osiadanie) dla pojedynczego pala jest tworzona w następujący sposób:
1) Graniczny tarcie na pobocznicy qs jest wyznaczane według wzoru:
![]()
gdzie: | a, b | - | |
vi | - | głębokość od powierzchni terenu do środka i-tej warstwy [m] | |
di | - | średnica pala w i-tej warstwie [m] |
natomiast opór (nośność) pobocznicy pala wyraża wzór:
![]()
gdzie: | m1 | - | |
m2 | - | ||
di | - | średnica pala w i-tej warstwie [m] | |
hi | - | miąższość i-tej warstwy [m] | |
qsi | - | graniczny opór (nośność) pobocznicy w i-tej warstwie [MPa] |
2) Nośność podstawy pala qb obliczana jest wg wzoru:
![]()
gdzie: | e, f | - | |
D | - | długość pala w gruncie [m] | |
db | - | średnica podstawy pala [m] |
3) Współczynnik obciążenia przenoszonego na podstawę pala β wyrażony jest za pomocą wzoru:
![]()
gdzie: | qb | - | nośność podstawy pala [MPa] |
| - | średnia ważona granicznego oporu (nośności) pobocznicy [MPa] | |
D | - | długość pala w gruncie [m] | |
db | średnica podstawy pala [m] |
Obciążenie aktywujące tarcie na pobocznicy Rsy wyraża wzór:
![]()
gdzie: | Rs | - | opór (nośność) pobocznicy pala [N] |
β | - | współczynnik obciążenia przenoszonego do podstawy pala [-] |
4) Obciążenie aktywujące opór Rsy wyraża wzór:
![]()
gdzie: | Is | - | |
Rsy | - | obciążenie w momencie mobilizacji tarcia na pobocznicy [N] | |
d | - | średnica pala [m] | |
Es | - | sieczny moduł odkształcenia otaczającego gruntu [MPa] |
5) Obciążenie w podstawie pala dla przyjętej wartości osiadania (dla granicznej wartości osiadania równej 25 mm) obliczane jest wg wzoru:
![]()
gdzie: | β | - | współczynnik obciążenia przenoszonego do podstawy pala [-] |
Rsy | - | obciążenie w momencie mobilizacji tarcia na pobocznicy [N] | |
slim | - | graniczna wartość osiadania (zwykle przyjmowana 25 mm) [m] | |
sy | osiadanie aktywujące opór pobocznicy [m] |
Opór pala dla danej wartości osiadania granicznego Slim wyrażony jest za pomocą wzoru:
![]()
gdzie: | Rblim | - | obciążenie w podstawie pala dla danej wartości osiadania [N] |
Rs | - | opór pobocznicy pala [N] |
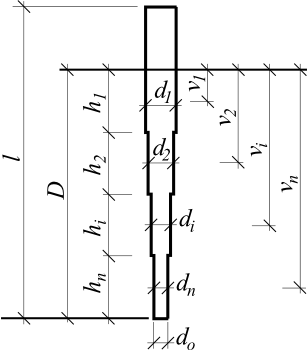 Podejście obliczeniowe według Masopusta
Podejście obliczeniowe według Masopusta
Literatura:
Masopust, J.: Vrtane piloty. 1st edition, Prague, Cenek a Jezek, 1994, 263 s.
Masopust, J., Glisnikova, V.: Zakladani staveb Modul M01. 1st edition, Brno, AN CERM, 2007, 182 s., ISBN 978-80-7204-538-9.